The Pythagorean Theorem is one of the most widely recognized and applied theorems in mathematics. Its simplicity and power have made it a cornerstone of geometry, appearing in various disciplines, including physics, engineering, computer science, and architecture. This theorem applies exclusively to right triangles, providing a direct relationship between the lengths of the sides.
1. Understanding the Pythagorean Theorem
The Pythagorean Theorem states:
\(a^2 + b^2 = c^2\)Here:
- a and b represent the lengths of the two legs of a right triangle.
- c represents the length of the hypotenuse, the side opposite the right angle.
The theorem asserts that the square of the hypotenuse’s length is equal to the sum of the squares of the lengths of the other two sides.
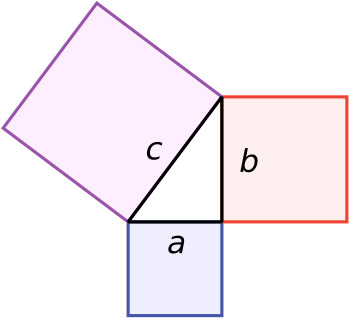
2. Visual Representation
To better understand this theorem, visualize a right triangle with sides labeled a, b, and c, where c is the hypotenuse.
This triangle illustrates how the sides a, b, and c relate to one another, fulfilling the equation \(a^2 + b^2 = c^2\).
3. Proof of the Pythagorean Theorem
The Pythagorean Theorem has numerous proofs—over 300 known, ranging from geometric to algebraic approaches. Below is one of the most common geometric proofs:
Geometric Proof
Consider a square constructed with side length \(a + b\), divided into four identical right triangles and a smaller central square. The area of the larger square can be expressed in two ways:
- The total area: \((a + b)^2\)
- The sum of the areas of the smaller square and four triangles: \(c^2 + 4 \cdot \frac{1}{2}ab\)
Equating these two areas:
\((a + b)^2 = c^2 + 2ab\)Expanding \((a + b)^2\):
\(a^2 + 2ab + b^2 = c^2 + 2ab\)Subtracting \(2ab\) from both sides:
\(a^2 + b^2 = c^2\)This concludes the proof.
4. Applications of the Pythagorean Theorem
The Pythagorean Theorem is widely applied across various fields, such as:
- Measuring Distances: It is used to find the distance between two points in a plane using the distance formula derived from the theorem.
- Construction and Architecture: Builders use it to ensure walls and foundations are square.
- Navigation and GPS: Helps calculate the shortest distance between two locations.
- Physics: Used to determine the resultant force in vector calculations.
5. Examples of the Pythagorean Theorem
Example 1: Finding the Hypotenuse
A triangle has legs \(a = 3\) and \(b = 4\). Find the hypotenuse \(c\).
\(c^2 = a^2 + b^2\) \(c^2 = 3^2 + 4^2 = 9 + 16 = 25\) \(c = \sqrt{25} = 5\)The hypotenuse is \(5\).
Example 2: Verifying a Right Triangle
A triangle has sides \(a = 5\), \(b = 12\), and \(c = 13\). Verify if it is a right triangle.
\(a^2 + b^2 = 5^2 + 12^2 = 25 + 144 = 169\) \(c^2 = 13^2 = 169\)Since \(a^2 + b^2 = c^2\), the triangle is a right triangle.
6. Pythagorean Triples
A Pythagorean triple consists of three positive integers \((a, b, c)\) satisfying the theorem \(a^2 + b^2 = c^2\). Common examples include:
- \((3, 4, 5)\)
- \((5, 12, 13)\)
- \((8, 15, 17)\)
Pythagorean triples can be generated using the formulas:
\(a = m^2 – n^2, \ b = 2mn, \ c = m^2 + n^2\)Here, \(m\) and \(n\) are positive integers where \(m > n > 0\).
The Pythagorean Theorem remains one of the most important tools in mathematics, offering insights into geometry, algebra, and real-world applications. Its elegance and simplicity have made it timeless and essential for students and professionals alike.